Grandeza escalar e Vetorial
Certas grandezas em física são traduzidas apenas por um número e sua unidade; esse número traduz a intensidade dessa grandeza. E só esse dado é suficiente para caracterizar tal grandeza.
Exemplo: 5kg de açúcar
Esse número e sua unidade são suficientes para definir a quantidade de açúcar, isto é, a grandeza massa fica perfeitamente caracterizada apernas por um número e sua unidade.
O mesmo acontece com a grandeza volume e temperatura. Veja:
• 2 litros de leite
• 37°C de temperatura
Então, as grandezas que ficam definidas apenas por um número e sua unidade são as grandezas escalares.
Mas, em certos casos, um número só não é capaz de traduzir o significado da grandeza.
Se aplicarmos uma força na bola de bilhar da figura, de modo que a bola sofra um deslocamento de 1 metro, só com esse número não podemos saber em que caçapa a bola vai cair.
Necessitamos de mais informações. Digamos que a bola vá se deslocar na direção vertical. A direção é a linha em que o deslocamento ocorre, e pode ser:
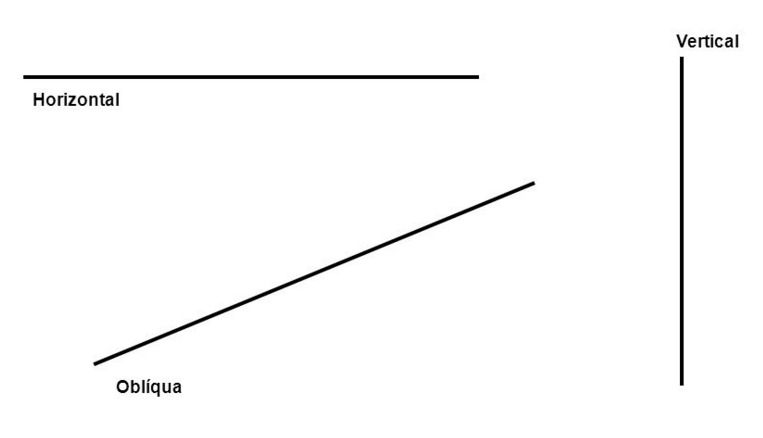Já sabemos o quanto a bola vai se deslocar, 1 metro na direção vertical; mas, mesmo com essas duas informações, ainda não podemos saber em caçapa a bola vai cair.
é preciso mais uma informação: o sentido em que o deslocamento vai ocorrer. Digamos que a bola vai ter direção vertical e para cima.
Portando, o sentido é uma das duas maneiras em que o corpo pode se deslocar em uma direção. é fácil notar que para cada direção podemos ter somente dois sentidos possíveis.
Veja:
O que causa maior ou menor deslocamento, é a intensidade da força aplicada.
As grandezas físicas que necessitam de três informações para serem caracterizadas, são as grandezas vetoriais. Vimos que essas informações são:
• Intensidade
• Direção
• Sentido
Portanto, força é uma grandeza vetorial, e fisicamente pode causar:
• Movimento de um corpo
• Modificar o movimento
• Deformação no corpo
Medindo Força - Dinamômetro
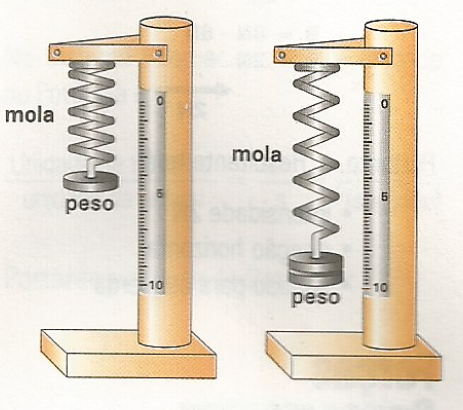O aparelho para medir intensidade de força é chamado de dinamômetro. Seu princípio é baseado na deformação de um material elástico — por exemplo, uma mola.
Observamos que a deformação da mola é proporcional ao peso que ela suporta.
Unidades de Força
Newton (N)
Um Newton (N) é a força que, aplicada a um corpo de massa 1kg, faz com que esse corpo tenha uma aceleração de 1 m/s².
Quilograma-Força (kgf)
Um Quilograma-Força (kgf) é a intensidade da força com que a Terra atrai um corpo de massa 1kg ao nível do mar.
Dina (dyn)
Um Dina (dyn) é a força que aplicada a um corpo de massa 1g, faz cin que esse corpo tenha uma aceleração de 1cm/s².
Transformando kgf em N:
1kgf = 9,8N, portanto basta pegar o número de kgf e multiplicar por 9,8.
Exemplo:
5kgf = 5 x 9,8 = 49N
Transformando N em kgf:
196N = 196 / 9,8 = 20kgf
Basta pegar e dividir a quantidade de Newstons (N) e dividir por 9,8.
E a Dina tem o seguinte valor:
1N = 100000 dyn
Vetor
A representação gráfica de uma grandeza vetorial é feita por um segmento de reta orientado, o qual fornece:
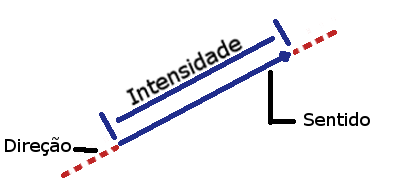
A intensidade é graficamente representada pelo tamanho do segmento em uma certa escala.
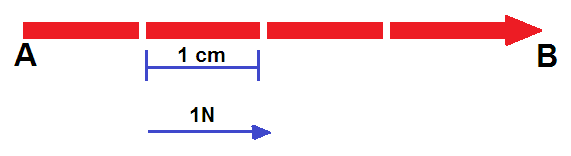
Vemos que na escala dada cada 1cm representa 1N.
A direção é determinada pela linha que apoia o vetor.
O sentido do vetor é dado pela ponta da seta.
Portanto o vetor AB tem intensidade de 4N (porque seu comprimento é 4cm), tem direção horizontal e sentido para direita.
Sistema de Forças
Quando em um corpo atuam várias forças, temos um sistema de forças e cada força desse sistema é chamada de componente do sistema.
As forças componentes podem ser substituídas por uma única força que provoca o mesmo resultado. Essa força recebe o nome de Força Resultante ou Vetor Soma.
Tipos de Sistema de Forças
Forças de :
Mesmo ponto de aplicação
Mesma direção
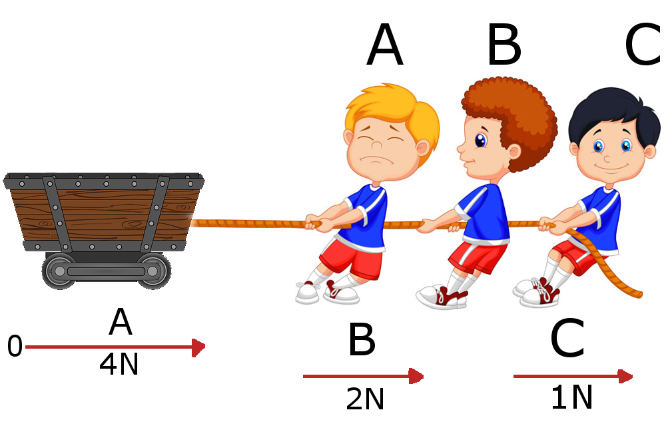
Nesse caso, para encontrarmos o vetor soma do sistema, somamos as forças componentes.
Veja:
R = 4N + 2N + 1N
R = 7N
—————————>
7N
Portanto, a resultante terá:
• intensidade 7N
• direção horizontal
• sentido para direita
Forças de :
Mesmo ponto de aplicação
Mesma direção
Sentido contrário
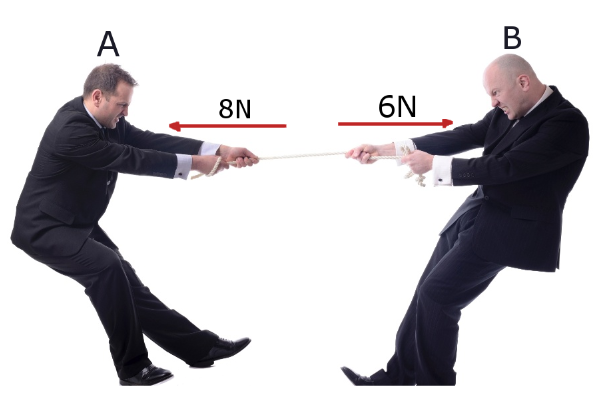
O vetor soma do sistema nesse caso serpa igual à diferença entre a componente de maior intensidade e a de menor intensidade. Ele terá o mesmo ponto de aplicação, mesma direção e o sentido da componente de maior intensidade.
Veja:
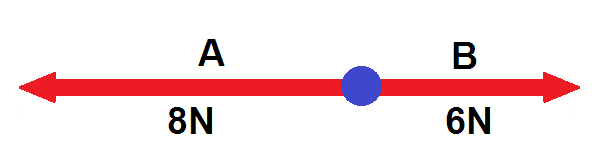
R = 8N - 6N
R = 2N
<———
2N
Portanto, a resultante terá:
• intensidade 2N
• direção horizontal
• sentido para esquerda
O vetor soma do sistema nesse caso serpa igual à diferença entre a componente de maior intensidade e a de menor intensidade. Ele terá o mesmo ponto de aplicação, mesma direção e o sentido da componente de maior intensidade.
Veja:
R = 8N - 6N
R = 2N
<———
2N
Portanto, a resultante terá:
• intensidade 2N
• direção horizontal
• sentido para esquerda
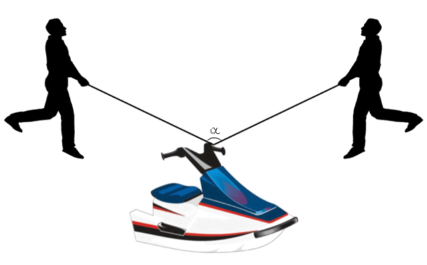
Forças Concorrentes
Forças concorrentes são aquelas em que as componentes formam um Ângulo no ponto de aplicação.
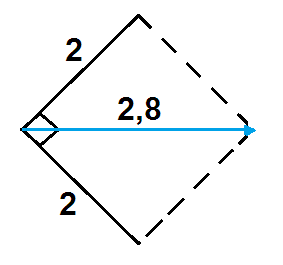
O vetor soma em forças concorrentes é representado em intensidade, direção e sentido pela diagonal do paralelogramo traçado sobre as componentes.
A intensidade é graficamente representada pelo tamanho da diagonal em uma escalada. Vemos na escalada dada que:
1N = 1cm
Como:
F1 = 2,0N, sua representação é um segmento de 2,0cm.
F2 = 2,0, sua representação é um segmento de 2,0cm.
Portanto a resultante ou o vetor soma tem intensidade de 2,8N, pois seu tamanho é 2,8cm.
Quando as forças concorrentes formam um ângulo de 90°, a intensidade do vetor soma pode ser encontrada aplicando-se o Teorema de Pitágoras, ou seja, pela fórmula:
R² = F1² + F2²
R² = √F1² + F2²
0 comentários:
Postar um comentário